Генерисање комбинаторних објеката
Проблеми се често могу решити исцрпном претрагом (грубом силом), што подразумева да се испитају сви могући кандидати за решења. Предуслов за то је да умемо све те кандидате да набројимо. Иако у реалним применама простор потенцијалних решења може имати различиту структуру, показује се да је у великом броју случаја то простор одређених класичних комбинаторних објеката: свих подскупова неког коначног скупа, свих варијација (са или без понављања), свих комбинација (са или без понављања), свих пермутација, свих партиција и слично. У овом поглављу ћемо проучити механизме њиховог систематичног генерисања. Нагласимо да по правилу оваквих објеката има експоненцијално много у односу на величину улаза, тако да су сви алгоритми практично неупотребљиви осим за веома мале димензије улаза.
Објекти се обично представљају \(n\)-торкама бројева, при чему се исти објекти могу торкама моделовати на различите начине. На пример, сваки подскуп скупа \(\{a_0, \ldots, a_{n-1}\}\) се може представити коначним низом индекса елемената који му припадају. Да би сваки подскуп био јединствено представљен, потребно је да тај низ буде канонизован (на пример, уређен строго растући). На пример, торка \((0, 2, 3)\) једнозначно одређује подскуп \(\{a_0, a_2, a_3\}\). Други начин да се подскупови представе су \(n\)-торке логичких вредности или вредности 0-1. На пример, ако је \(n=6\), и ако претпоставимо да се битови слева надесно, тада торка \(1011\) означава скуп \(\{a_0, a_2, a_3\}\).
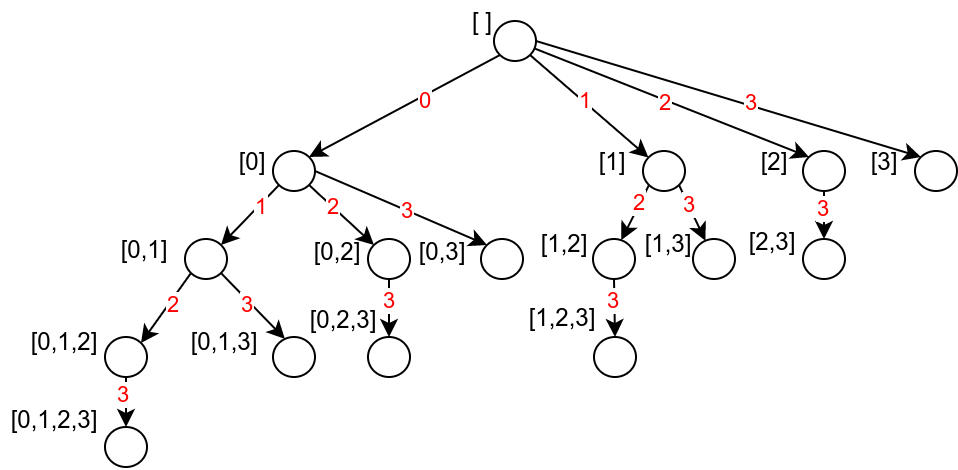
Сви објекти се обично могу представити дрветом и то дрво одговара процесу њиховог генерисања тј. обиласка (оно се не прави експлицитно, у меморији, али нам помаже да разумемо и организујемо поступак претраге). Обилазак дрвета се најједноставније изводи у дубину (често рекурзивно). За прву наведену репрезентацију подскупова дрво је дато на слици \(\ref{podskupovi-drvo-1}\). Сваки чвор дрвета одговара једном подскупу, при чему се одговарајућа торка очитава на гранама пута који води од корена до тог чвора.
За другу наведену репрезентацију подскупова дрво је дато на слици \(\ref{podskupovi-drvo-2}\). На почетку се бира да ли ће елемент \(a_0\) бити укључен у подскуп, на наредном нивоу да ли ће бити укључен елемент \(a_1\), затим елемент \(a_2\) и тако даље. Само листови дрвета у којима је за сваки елемент донета одлука да ли припада или не припада подскупу, одговарају подскуповима, при чему се одговарајућа торка логичких вредности очитава на гранама пута који води од корена до тог чвора.
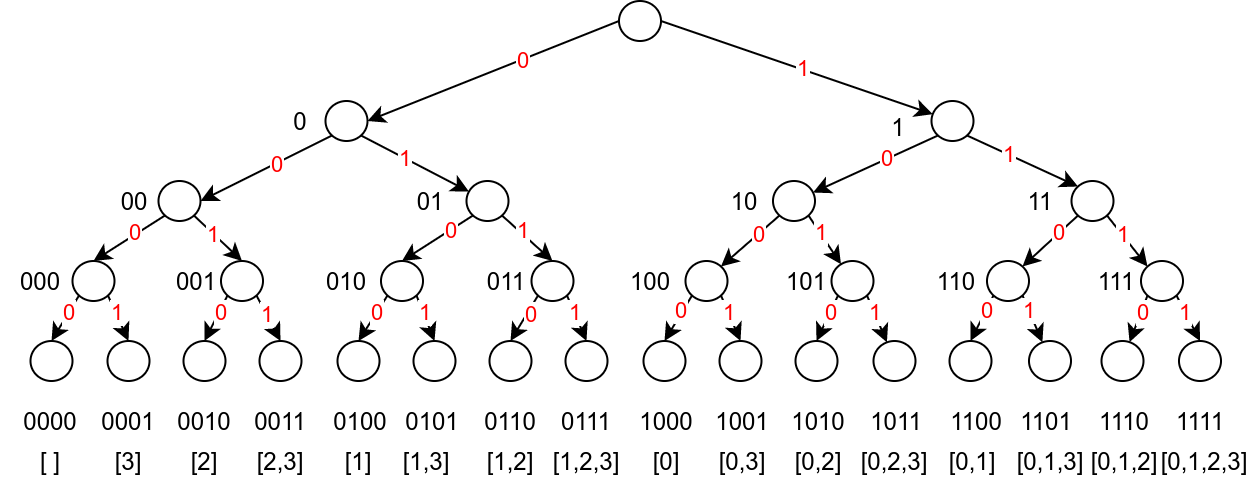
Приметимо да оба дрвета садрже \(2^n\) чворова којима се представљају подскупови (у првом случају су то сви чворови дрвета, а у другом само листови).
Приликом генерисања објеката често је пожељно ређати их одређеним редом. С обзиром на то то да се сви комбинаторни објекти представљају одређеним торкама (коначним низовима), природан поредак међу њима је лексикографски поредак (који се користи за утврђивање редоследа речи у речнику). Подсетимо се, торка \(a_0\ldots a_{m-1}\) лексикографски претходи торци \(b_0\ldots b_{n-1}\) акко постоји неки индекс \(i\) такав да за свако \(0 \leq j < i\) важи \(a_j = b_j\) и важи или да је \(a_i < b_i\) или да је \(i = m < n\). На пример важи да је \(11 < 112 < 221\) (овде је \(i=2\), а затим \(i=0\)).
На пример, ако подскупове скупа \(\{1, 2, 3\}\) представимо на први начин, торкама у којима су елементи уређени растуће, лексикографски поредак би био \(\emptyset\), \(\{1\}\), \(\{1, 2\}\), \(\{1, 2, 3\}\), \(\{1, 3\}\), \(\{2\}\), \(\{2, 3\}\), \(\{3\}\). Ако бисмо их представљали на други начин, торкама у којима се нулама и јединицама одређује да ли је неки елемент укључен у подскуп, лексикографски редослед би био: 000 (\(\emptyset\)), 001 (\(\{3\}\)), 010(\(\{2\}\)), 011(\(\{2, 3\}\)), 100(\(\{1\}\)), 101(\(\{1,3\}\)), 110(\(\{1,2\}\)) и 111(\(\{1,2,3\}\)).
У наставку ће бити приказано како је могуће набројати све објекте који имају неку задату комбинаторну структуру. У већини задатака могуће је разматрати две врсте решења. Једна група решења је заснована на рекурзивном поступку набрајања објеката, док је друга група решења заснована на проналажењу наредног комбинаторног објекта у односу на неки задати редослед (најчешће лексикорафски).
